零基础跟了老师一个月,思维导图不会弄,期间学了一些算法可以做一些分享,请大家指正
查找长度:关键码的比较次数,评估查找算法的性能
1. 二分查找法的一般写法
class BinarySearch1 { // high设置为数组下标末端的后一位,即为arr.length,最后会分析原因
public int search(int[] arr, int key, int low, int high) {
while (low <= high) {
int mid = (low + high) / 2;
int midVal = arr[mid];
// 这里的判断条件如果先是key == midVal,判断的次数会更多,算法性能会下降
if (key < midVal) {
high = mid - 1;
}else if(midVal < key){
low = mid + 1;
}else{
return mid;
}
}
return -1;
}
}查找长度分析:每一次判断,如果目标值在midVal左侧,只需要进行一次判断就可以转向,但是目标值在midVal右侧,需要进行两次判断才可以转向。
如果将第一个条件判断语句改为key == midVal ,则无论目标值在左侧和右侧都需要两次判断,这样反而会降低效率。
查找长度的精确计算
我们不妨设定high与low的差值为2^k,那么数组长度为2^k-1。其中设C(k-1)总体查找长度,当进行一次二分查找时,当降维为C(k-1)时,左侧每个元素少比较一次,右侧每个元素少比较两次,如果命中还需两次比较。综上得出如下表达式: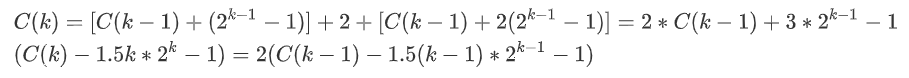
用数列不断向下迭代,由C(1)= 2可以得出一般通式,然后除以元素个数得出每个元素被取到的平均长度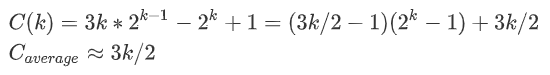
将n带入得到二分查找法的时间复杂度为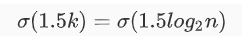
优化的思考
-
目标值左侧转向需要一次判断,目标值右侧转向需要二次判断,既然左侧判断成本低,分割点往右侧移动会整体降低判断成本。
- 分割点的位置应该设在哪里?
2. 黄金分割查找算法(斐波那契查找算法)
分割点位置分析
对优化思路进行抽象:计算稍微有点麻烦,还可以接受
总体来看,黄金分割查找算法对普通的二分查找算法起到了优化效果,是在常系数上起到了作用
// 斐波那契查找算法
public class FibSearch {
// 构造斐波那契数列,可以用动态规划法对其优化
public static int[] fib() {
int[] f = new int[20];
f[0] = 1;
f[1] = 1;
for (int i = 2; i < 20; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
// 实现斐波那契排序算法
public static int fibSearch(int[] arr, int key, int low, int high) {
int k = 0;
int mid = 0;
int f[] = fib();
while (high > f[k]) {
k++;
}
int[] temp = Arrays.copyOf(arr, f[k]);
for (int i = high; i < temp.length; i++) {
temp[i] = arr[high - 1];
}
while (low <= high) {
mid = low + f[k - 1] - 1;
if (key < temp[mid]) { // 判断要先判断左侧,来让左侧转向发挥最大效用
high = mid;
k--;
} else if (key > temp[mid]) {
low = mid + 1;
k -= 2;
} else {
if (mid < high) {
return mid;
} else {
return high - 1;
}
}
}
return -1;
}
}优化的思考
上面两种查找算法比较类似快速排序分区的想法,都是如果正好找到值则立马结束,返回下标位置,但也正是因为如此造成了查找长度的不平衡。
3. 二分查找法的优化
优化的思路
为了平衡查找长度,我们可以借鉴归并排序的想法,直接将数组一分为二,即使能命中目标值,也不急于返回,从整体上提升性能
class BinarySearch2{
public int search(int[] arr, int key, int low, int high) {
while (low + 1 < high) {
int mid = (low + high) / 2;
int midVal = arr[mid];
if (key < midVal) {
high = mid;
}else if(midVal < key){
low = mid;
}
}
return (key == arr[low])? key : -1 ;
}
}查找长度精确计算:与第一种方法类似,我这里直接写结果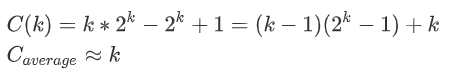
将n带入得到二分查找法的时间复杂度为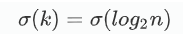
综合来看:两种二分查找法比较来看,后者在最好的情况下不如前者,最坏的情况下优于前者,但时间复杂度整体上得到优化
优化的思考
- 第二种二分查找法似乎已经到了优化的极限,但是二分查找的目标不仅仅在于找到,还有一个关键是没找到时该返回何种数值
- 当查找的数字不在数组中或者查找的目标个数存在多个,我们希望返回的值能为key的插入提供指导,比如key有多个,返回最后一个;key比整体小,则返回头部的位置; key比整体大,则返回尾部的位置
- while中的判断方法low + 1 < high这种判断方法对上述的情况有助力吗?
4. 二分查找的最终优化
优化的思路
- 数轴的表示方式,在数轴上表示数细想起来还是有挺多细节的,在整数数组中,对于一个数字2,[2,3)表示一个2,在数轴上表示为一段区间,[2,2)表示一条线,在数轴上表示2区间的前界,同时也是1区间的后界。同理[3,3)表示2区间的后界。
- 一般都会采取前界或者一个区间来表示一个数的具体位置,但在当下这个场景并非最好的选择。特别是碰到多个相同key元素时为后续插入位置提供位点时,只有通过后界来跳出循环才能实现。
- 通过数字后界来返回数组能完美解决key在数组左右侧,多次出现的问题,为后续的插入位置提供方向,只需在返回值+1即可。
- high之所以选择arr.length而不是arr.length-1,是为了服务key大于数组所有元素,保证插入位置的准确。
class BinarySearch3 {
public int search(int[] arr, int key, int low, int high) {
while (low < high) {
int mid = (low + high) / 2;
int midVal = arr[mid];
if (key < midVal) {
high = mid;
}else{
low = mid + 1; // 代码的核心
}
}
return --low;
}
}总体分析:目前是二分查找最终优化版本,在算法性能和返回值上都很不错。
5. Java的二分查找的源码分析
private static int binarySearch0(int[] a, int fromIndex, int toIndex,
int key) {
int low = fromIndex;
int high = toIndex - 1;
while (low <= high) {
int mid = (low + high) >>> 1;
int midVal = a[mid];
if (midVal < key)
low = mid + 1;
else if (midVal > key)
high = mid - 1;
else
return mid; // key found
}
return -(low + 1); // key not found.
}源码的分析
- 从时间复杂度来看,并没有做到最优化
- 从意外返回值的类型来分析
- 如果key在数组左侧,返回值 -1
- 如果key在数组右侧,返回值为为负数
- 如果存在多个key值,无法返回key最末端元素
- 此种返回值的好处为找到为整数,没找到为负数,这是优势的地方。


